Volumen orientado

En esta entrada intentaré replicar las clases de la última semana en las que utilizamos las propiedades del volumen de un paralelepípedo dado por tres vectores, para obtener una fórmula explícita del mismo.

Notación y preliminares

Antes de comenzar con la deducción de la fórmula, tomemos un momento para fijar la notación y repasar las nociones básicas involucradas.

Recordemos que estamos trabjando en el espacio, hemos fijado un origen \(\mathcal{O}\), y cualquier punto del espacio \(P\) determina un vector que inicia en el origen y termina en \(P\).

Usando la ley del paralelogramo podemos definir la suma de vectores; la multiplicación de un vector por un número real es un poco más difícil de definir, pero se reduce a una aplicación ingeniosa del teorema de Tales.

El conjunto de todos los vectores junto con las operaciones de suma y de multiplicación por un número real, satisfacen las propiedades usuales. Para ver una lista detallada de las propiedades, véase la entrada en wikipedia sobre espacios vectoriales.

Además el vector cero, que escribimos como \(\vec 0\) es el único vector que empieza y termina en el origen, y que satisface \(\vec 0 +\vec v = \vec v\) para cualquier otro vector \(\vec v\).

Paralelepípedos

Sean \(\vec v, \vec w, \vec z\) tres vectores. Los puntos finales de los vectores

\[\vec 0, \vec v, \vec w, \vec z, \vec v+\vec w, \vec v +\vec z, \vec w +\vec z, \vec v+ \vec w + \vec z\]

forman los vértices de un paralelepípedo, tres de cuyos lados están dados por los vectores \(\vec v, \vec w, \vec z\). Decimos que dicho paralelepípedo está generado, o determinado, por los tres vectores.

Estamos interesados en encontrar una manera general para calcular el volumen del paralelepípedo determinado por cualquier terna de vectores.

Por el momento usaremos una noción intuitiva de volumen. Sin embargo, a pesar de no dar una definición explícita, hay ciertas propiedades que cualquier definición sensata de volumen debería cumplir.

Denotaremos el volumen del paralelepípedo generado por los vectores \(\vec v, \vec w, \vec z\) por \(V(\vec v, \vec w, \vec z)\). Abusando ligeramente la notación, hablaremos del volumen de los tres vectores cuando realmente nos referimos al volumen del paralelepípedo que ellos generan.

Propiedades deseables del volumen

En términos más técnicos, el volumen \(V\) debería ser una función que recibe como entrada tres vectores y produce como resultado un real.

Decir que el volumen es una función simplemente quiere decir que dados cualesquiera tres vectores, hay una manera sin ambigüedades de producir un número real al que llamamos el volumen, y dicho número real únicamente depende de los tres vectores.

En principio, nos gustaría encontrar una definición de volumen que además, siempre produzca números positivos, pues el volumen es una cantidad positiva, sin embargo, como veremos un poco más adelante, este requerimiento entra en contradicción con otra propiedad igual de deseable.

Dejemos por ahora el asunto de la positividad del volumen.

Como es usual cuando definimos alguna cantidad que tiene que ver con vectores (como el producto interno) una de las primeras preguntas que surgen es si esa cantidad interactua apropiadamente con la suma de vectores.

Dicho de otro modo, ¿habrá alguna relación entre \(V(\vec v+ \vec v^\prime, \vec w, \vec z)\) y las cantidades \(V(\vec v, \vec w, \vec z), V(\vec v^\prime, \vec w, \vec z)\)?

Experimentando un poco con ejemplos sencillos, como por ejemplo \(V(\vec v+ \vec v, \vec w, \vec z)\) que debería ser el doble que \(V(\vec v, \vec w, \vec z)\), pues simplemente duplicamos uno de los lados del paralelepípedo, no es difícil convencerse de que sería deseable que

\[V(\vec v+ \vec v^\prime, \vec w, \vec z)= V(\vec v, \vec w, \vec z)+ V(\vec v^\prime, \vec w, \vec z)\]

siempre fuera cierto.

Así mismo, multiplicar un vector por un escalar positivo, tiene el efecto de cambiar la longitud de dicho vector por un factor que es igual al escalar, por lo que cambiaría el volumen del paralelepípedo por ese mismo factor.

Dicho de otro modo, la identidad

\[V(\lambda\vec v, \vec w, \vec z)= \lambda V(\vec v, \vec w, \vec z)\]

también es razonable.

Notemos que el uso de la primera variable en las propiedades arriba mencionadas realmente no es relevante, por lo que propiedades análogas se deben cumplir para la segunda y tercera variable, aunque siempre dejando fijas a las otras dos varialbles.

Finalmente, si los tres vectores son coplanares, es decir, uno de ellos es combinación lineal de los otros dos, el paralelepípedo que generan está contenido en un plano, por lo que no tiene volumen, en símbolos:

\[V(\lambda\vec w+ \mu\vec z, \vec w, \vec z)=0\]

En particular, si de los tres vectores dos son iguales, el volumen debe ser cero: \(V(\vec w, \vec w, \vec z)=0\).

Ahora bien, volvamos al tema de la positividad del volumen:

Si suponemos que \(V\) ya ha sido definido y cumple las propiedades arriba mencionadas, entonces, para cualesquiera tres vectores \(\vec v, \vec w, \vec z\), se debe cumplir:

\(0 = V(\vec v+ \vec w, \vec v +\vec w, \vec z)=\) \(V(\vec v, \vec v + \vec w, \vec z)+ V(\vec w,\vec v+ \vec w, \vec z) =\) \(V(\vec v, \vec v, \vec z)+ V(\vec v , \vec w, \vec z) +\) \(V(\vec w, \vec v, \vec z)+ V(\vec w, \vec w, \vec z)\)

notemos que de los últimos cuatro términos, dos tienen vectores repetidos, por lo que son iguales a cero, es decir, obtenemos la identidad:

\[0 = V(\vec v, \vec w, \vec z)+ V(\vec w, \vec v, \vec z)\]

o lo que es lo mismo:

\[V(\vec v, \vec w, \vec z)=- V(\vec w, \vec v, \vec z)\]

¡al intercambiar dos variables, el volumen cambia de signo!

Es por esto que sin importar cómo definamos el volumen, si queremos que cumpla ciertas propiedades deseables, necesariamente tenemos que permitir volúmenes negativos.

Las tres propiedades que no se pueden cumplir simultánemente son:

• Aditividad
• Positividad
• El volumen es cero si los tres vectores son coplanares

La tercera es realmente importante: no queremos que nada que esté contenido en un plano tenga volumen diferente de cero.

Sobre las primeras dos, alguien podría argumentar que es mejor tener positividad, y que aditividad es pedir demasiado, sin embargo, resulta que la teoría que se desarrolla es mucho más fructífera si abandonamos la positividad del volumen.

Hay una última propiedad que será importante. Hay que recordar que las bases ortonormales eran muy útiles pues permiten expresar fácilmente a cualquier vector con coordenadas, por lo que es natural pensar que utilizando de algún modo una base ortonormal se podría simplificar el cálculo del volumen.

En lo sucesivo fijaremos una base ortonormal \(\beta = \{\vec w_1, \vec w_2,\vec w_3\}\). Esto quiere decir que los tres vectores \(\vec w_1, \vec w_2,\vec w_3\) son ortogonales dos a dos y que todos tienen longitud uno. Así mismo, cualquier vector \(\vec v\) se puede expresar como

\[\vec v = \langle \vec v, \vec w_1\rangle\vec w_1 + \langle \vec v, \vec w_2\rangle\vec w_2 +\langle \vec v, \vec w_3\rangle\vec w_3\]

y además, definimos las coordenadas de \(\vec v\) con respecto a la base \(\beta\) como la terna de números:

\[\vec v_\beta = \left(\langle \vec v, \vec w_1\rangle, \langle \vec v, \vec w_2\rangle, \langle \vec v, \vec w_3\rangle\right) \in \mathbb{R}^3\]

Finalmente, la última propiedad es bastante natural: los vectores \(\vec w_1,\vec w_2,\vec w_3\) forman las aristas de un cubo de lado uno, por lo que sería natural que

\[V(\vec w_1,\vec w_2,\vec w_3) =1\]

Fórmula para el volumen

En esta sección obtendremos una fórmula explícita con la que podemos definir el volumen. Sin embargo, dado que la fórmula no es obvia, empezaremos al revés: supondremos que el volumen ya ha sido definido y que cumple ciertas propiedades para eventualmente deducir una fórmula.

Para fijar ideas, escribamos lo anterior formalmente.

Sea \(V\) una función que recibe como entrada una terna de vectores y produce como salida un número real. Supongamos que la función \(V\) satisface las siguientes propiedades:

• Multilinealidad:

  \[V(\vec v+ \lambda\vec v^\prime, \vec w, \vec z)= V(\vec v, \vec w, \vec z)+ \lambda V(\vec v^\prime, \vec w, \vec z)\] \[V(\vec v, \vec w +\lambda \vec w^\prime, \vec z)= V(\vec v, \vec w, \vec z)+ \lambda V(\vec v, \vec w^\prime, \vec z)\] \[V(\vec v, \vec w, \vec z+ \lambda\vec z^\prime)= V(\vec v, \vec w, \vec z)+ \lambda V(\vec v, \vec w, \vec z^\prime)\]

• Alternancia:

\[V(\vec v, \vec w, \vec z)= - V(\vec w, \vec v, \vec z)\] \[V(\vec v, \vec w, \vec z)= - V(\vec z, \vec w, \vec v)\] \[V(\vec v, \vec w, \vec z)= - V(\vec v, \vec z, \vec w)\]

• Normalización

  \[V(\vec w_1,\vec w_2,\vec w_3) =1\]

Supongamos además que los tres vectores \(\vec v, \vec w, \vec z\) expresados en la base \(\beta\), tienen coordenadas:

\[\vec v_\beta = (a,b,c)\] \[\vec w_\beta = (d,e,f)\] \[\vec z_\beta = (g,h,i)\]

Notemos que como las coordenadas determinan y están determinadas por los vectores, y además dependen linealmente de ellos, en vez de escribir

\[V(\vec v, \vec w, \vec z)= V\left(a \vec w_1+b\vec w_2+c\vec w_3,~d\vec w_1+e\vec w_2+f\vec w_3 ,~g\vec w_1+h\vec w_2+i\vec w_3 \right)\]

Podríamos escribir simplemente

\(V( (a,b,c),(d,e,f),(g,h,i))\) o, usando una notación más compacta y escribiendo las coordenadas de un vector verticalmente:

\[{\Large V} \left ( \begin{matrix} a & d & g \\ b & e & h \\ c & f & i \end{matrix} \right)\]

Exploremos brevemente la forma que deben tomar las propiedades del volumen con esta nueva notación. Por ejemplo, el primer inciso de la multilinealidad, ahora dice:

\[{\Large V} \left ( \begin{matrix} a +\lambda a^\prime & d & g \\ b +\lambda b^\prime& e & h \\ c +\lambda c^\prime & f & i \end{matrix} \right) = {\Large V} \left ( \begin{matrix} a & d & g \\ b & e & h \\ c & f & i \end{matrix} \right)+ {\Large \lambda V} \left ( \begin{matrix} a^\prime & d & g \\ b^\prime & e & h \\ c^\prime & f & i \end{matrix} \right)\]

La alternancia, ahora corresponde a:

\[{\Large V} \left ( \begin{matrix} a & d & g \\ b & e & h \\ c & f & i \end{matrix} \right)= {\Large -V} \left ( \begin{matrix} d & a & g \\ e & b & h \\ f & c & i \end{matrix} \right)\]

finalmente, la normalización es la igualdad

\[{\Large V} \left ( \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right)= 1\]

Una consecuencia inmediata de la multilinealidad y la alternancia es que:

\[{\Large V} \left ( \begin{matrix} a & d+ \lambda a & g \\ b & e+ \lambda b & h \\ c & f+ \lambda c & i \end{matrix} \right)= {\Large V} \left ( \begin{matrix} a & d & g \\ b & e & h \\ c & f & i \end{matrix} \right) + {\Large \lambda V} \left ( \begin{matrix} a & a & g \\ b & b & h \\ c & c & i \end{matrix} \right)\] \[={\Large V} \left ( \begin{matrix} a & d & g \\ b & e & h \\ c & f & i \end{matrix} \right)\]

es decir, podemos sumar cualquier múltiplo del primer vector al segundo sin alterar el volumen. Una fórmula similar usando las demás variables muestra que podemos sumar un multiplo de cualquier entrada a cualquier otra entrada distinta. Geométricamente, esto representa que si deslizamos paralelamente la tapa superior de un paralelepípedo, no alteramos su volumen:

Ahora bien, para obtener la fórmula buscada, comenzaremos utilizando la multilinealidad en la primera entrada para intentar simplificar el volumen:

\[{\Large V} \left ( \begin{matrix} a & d & g \\ b & e & h \\ c & f & i \end{matrix} \right)= {\Large a V} \left ( \begin{matrix} 1 & d & g \\ 0 & e & h \\ 0 & f & i \end{matrix} \right) + {\Large b V} \left ( \begin{matrix} 0 & d & g \\ 1 & e & h \\ 0 & f & i \end{matrix} \right) + {\Large c V} \left ( \begin{matrix} 0 & d & g \\ 0 & e & h \\ 1 & f & i \end{matrix} \right)\]

nótese que en cada uno de los tres sumandos de arriba, la primera entrada es un vector de la base ortonormal, es decir, estamos descomponiendo el volumen original como suma de tres volúmenes, cada uno de los cuales corresponde a un paralelepípedo con al menos una arista alineada con un elemento de la base ortonormal.

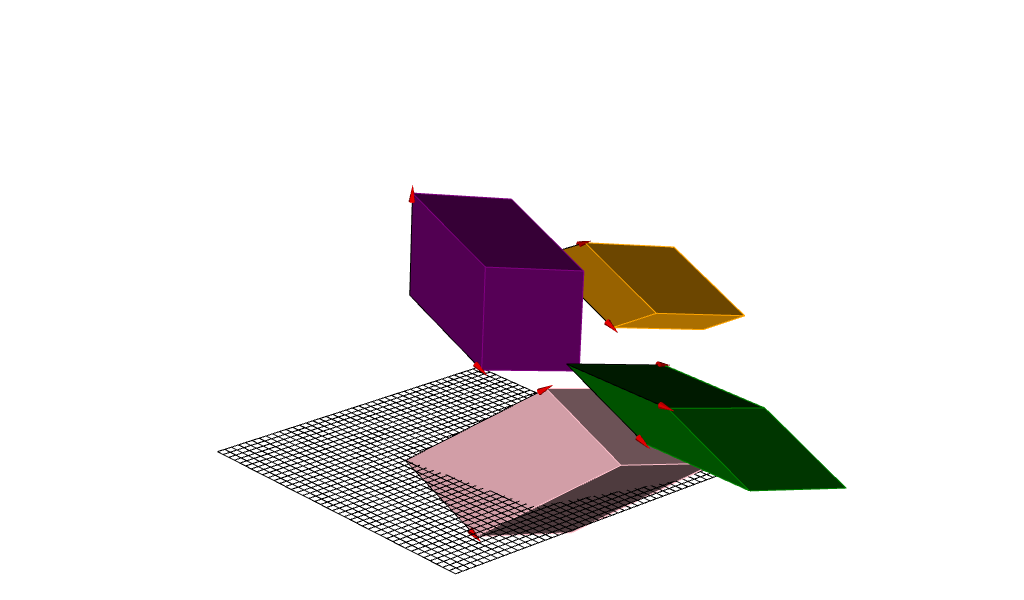
En las siguientes dos animaciones, podemos ver cómo se descompone el volumen rosa como suma de los tres volúmenes verde, naranja y púrpura, mismos que salvo un desplazamiento paralelo de si tapa superior, tienen una arista alineada con los ejes del sistema de coordenadas: el púrpura tiene una arista en la dirección vertical, mientras que los paralelepípedos naranja y verde tienen una arista en cada una de las direcciones del plano de referencia.

Cada uno de los sumandos que que aparecieron pueden ser simplificados aún más, pues podemos sumar un múltiplo arbitrario de la primera entrada a las otras dos, por ejemplo, el primer sumando se simplifica de la siguiente manera:

\[{\Large a V} \left ( \begin{matrix} 1 & d & g \\ 0 & e & h \\ 0 & f & i \end{matrix} \right) = {\Large a V} \left ( \begin{matrix} 1 & d+ (-d)1 & g+ (-g)1 \\ 0 & e+ (-d)0 & h+ (-g)0 \\ 0 & f+ (-d)0 & i+ (-g)0 \end{matrix} \right) = {\Large a V} \left ( \begin{matrix} 1 & 0 & 0 \\ 0 & e & h \\ 0 & f & i \end{matrix} \right)\]

Es decir, utilizando la primera entrada, que es el primer vector de la base, podemos deslizar los otros dos vectores hasta que estén en el plano perpendicular al vector \(\vec w_1\), es decir, en el plano generado por \(\vec w_1\) y \(\vec w_2\). De manera totalmente análoga, el segundo y tercer sumando se simplifican a:

\[{\Large b V} \left ( \begin{matrix} 0 & d & g \\ 1 & 0 & 0 \\ 0 & f & i \end{matrix} \right) ~~,~~ {\Large c V} \left ( \begin{matrix} 0 & d & g \\ 0 & e & h \\ 1 & 0 & 0 \end{matrix} \right)\]

En la siguiente animación, simplemente desplazamos los tres paralelepípedos con tal de que se pueda apreciar mejor el deslizamiento que se aplica en la segunda animación.

Aquí podemos ver como en cada paralelepípedo, los dos vectores que no están alineados con uno de los ejes, son deslizados en esa dirección hasta que caen en el plano perpendicular al eje. Por ejemplo, en el caso del paralelepípedo púrpura, que tiene una arista alineada con el eje vertical, los otros dos vectores se deslizan verticalmente hasta que son paralelos al plano horizontal.

Con esto es claro que hemos reducido el problema a calcular el volumen de ciertos paralelepípedos muy particulares: una de sus aristas es uno de los elementos de la base ortonormal, mientras que los otros dos son perpendiculares a este. Así, es de esperarse que el volumen resulte el producto de el área que definen los dos ultimos vectores por la longitud del primero, en cierto modo, recuperamos la fórmula elemental de “área de la base por altura”.

Veamos una demostración formal de este hecho, al menos para el primer sumando:

\[{\Large a V} \left ( \begin{matrix} 1 & 0 & 0 \\ 0 & e & h \\ 0 & f & i \end{matrix} \right) = {\Large ae V} \left ( \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & h \\ 0 & 0 & i \end{matrix} \right) + {\Large af V} \left ( \begin{matrix} 1 & 0 & 0 \\ 0 & 0 & h \\ 0 & 1 & i \end{matrix} \right)\] \[={\Large ae V} \left ( \begin{matrix} 1 & 0 & 0+(-h)0 \\ 0 & 1 & h+(-h)1 \\ 0 & 0 & i+(-h)0 \end{matrix} \right) + {\Large af V} \left ( \begin{matrix} 1 & 0 & 0+(-i)0 \\ 0 & 0 & h+(-i)0 \\ 0 & 1 & i+(-i)1 \end{matrix} \right)\] \[={\Large ae V} \left ( \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & i \end{matrix} \right) + {\Large af V} \left ( \begin{matrix} 1 & 0 & 0 \\ 0 & 0 & h \\ 0 & 1 & 0 \end{matrix} \right)\]

en la penultima igualdad usamos el hecho de que podemos sumar un múltiplo adecuado de la segunda entrada a la tercera. Finalmente, utilizando las propiedad de normalización y alternancia, podemos simplificar por completo la última cantidad:

\[={\Large ae V} \left ( \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & i \end{matrix} \right) + {\Large af V} \left ( \begin{matrix} 1 & 0 & 0 \\ 0 & 0 & h \\ 0 & 1 & 0 \end{matrix} \right)\] \[={\Large aei V} \left ( \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right) - {\Large afhV} \left ( \begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix} \right)\] \[aei - afh = a(ei-fh)\]

Notemos que la cantidad \(ei-fh\) es precisamente el área del paralelogramo definido por los vectores \(e\vec w_2 +f\vec w_3\) y \(h\vec w_2+i\vec w_3\), que son justamente las proyecciones de \(\vec w\) y \(\vec z\) al plano perpendicular a \(\vec w_1\). Es decir, hemos demostrado:

\[{\Large V} \left ( \begin{matrix} a & 0 & 0 \\ 0 & e & h \\ 0 & f & i \end{matrix} \right) = {\Large a A} \left ( \begin{matrix} e & h \\ f & i \end{matrix} \right)\]

donde

\[{\Large A} \left ( \begin{matrix} e & h \\ f & i \end{matrix} \right) = ei-hf\]

De manera totalmente análoga, se pueden obtener fórmulas similares para los otros dos sumandos que habíamos obtenido, sin embargo, algo que no es obvio a primera vista, pero que al hacer las cuentas detalladamente resulta claro, es que el segundo sumando aparece con un signo menos. Finalmente, combinando todo lo anterior, obtenemos:

\[{\Large V} \left ( \begin{matrix} a & d & g \\ b & e & h \\ c & f & i \end{matrix} \right)= {\Large a V} \left ( \begin{matrix} 1 & d & g \\ 0 & e & h \\ 0 & f & i \end{matrix} \right) + {\Large b V} \left ( \begin{matrix} 0 & d & g \\ b & e & h \\ 0 & f & i \end{matrix} \right) + {\Large c V} \left ( \begin{matrix} 0 & d & g \\ 0 & e & h \\ 1 & f & i \end{matrix} \right)\] \[= {\Large a A} \left ( \begin{matrix} e & h \\ f & i \end{matrix} \right) - {\Large b A} \left ( \begin{matrix} d & g \\ f & i \end{matrix} \right) + {\Large c A} \left ( \begin{matrix} d & g \\ e & h \end{matrix} \right)\] \[=a(ei-hf) - b(di-gh) + c(dh-eg)\]

Es decir, obtuvimos una fórmula para el volumen que está expresada únicamente en términos de las coordenadas de los vectores con respecto a la base ortonormal.

Como todo lo anterior fue suponiendo la existencia de una función \(V\) que cumpliera ciertas propiedades, ahora podemos volver al inicio y definir el volumen mediante dicha fórmula:

\[{\Large V} \left ( \begin{matrix} a & d & g \\ b & e & h \\ c & f & i \end{matrix} \right) =a(ei-hf) - b(di-gh) + c(dh-eg)\]

No es difícil demostrar que el volumen así definido cumple que es multilineal, alternante y que al evaluarlo en \(\vec w_1,\vec w_2,\vec w_3\) vale 1, por lo que efectivamente provee de una definición sensata de volumen.

Unicidad del volumen

Solo resta mencionar una consecuencia inesperada de lo que hicimos anteriormente.

Al deducir la fórmula para el volumen, únicamente utilizamos que fuese una función bien definida y que cumpliera ciertas propiedades, y al final, obtuvimos una fórmula que no depende más que de las coordenadas de los vectores, por lo que, si tuvieramos otra definición alternativa para el volumen, pero que cumple las mismas propiedades, las dos definiciones deberían ser expresables en términos de la misma fórmula,es decir, serían exactamente iguales.

En términos más sencillos, simplemente diremos que el volumen es único, y a pesar de que este hecho parezca obvio o poco relevante, lo utilizaremos con frecuencia más adelante.

Referencias y generalizaciones

La fórmula que obtuvimos para el volumen es un caso particular del teorema de Laplace, que en general habla de determinates de matrices.

Probablemente muchos reconozcan en la fórmula el cálculo de un determinante de una matríz de 3 por 3. Así mismo, las áreas que aparecen son determinantes de matrices de 2 por 2. Efectivamente, una posible manera de generalizar esto es utilizando determinantes de matrices de \(n\) por \(n\).

Los determinantes tienen aplicaciones en inumerables áreas, y más en general, no solo sirven para calcular volúmenes, sino para describir el comportamiento de ciertas transformaciones: las transformaciones lineales.

La unicidad del volumen es un hecho que también se puede generalizar:

Dado un espacio vectorial de dimensión \(n\), y una base fija \(\beta = \{\vec v_1, \ldots, \vec v_n\}\), existe una única función \(V\) que es \(n-\)lineal, alternante y tal que \(V(\vec v_1, \ldots, \vec v_n)= 1\)

En términos mucho más abstractos, se dice que la enésima potencia exterior de un espacio vectorial de dimensión \(n\) es de dimensión \(1\).

Publicado el 17 de marzo de 2018 por Román Contreras